Heat equation solver¶
In this example we will solve the heat equation using the EDO solver from scipy. A typical result is shown below :
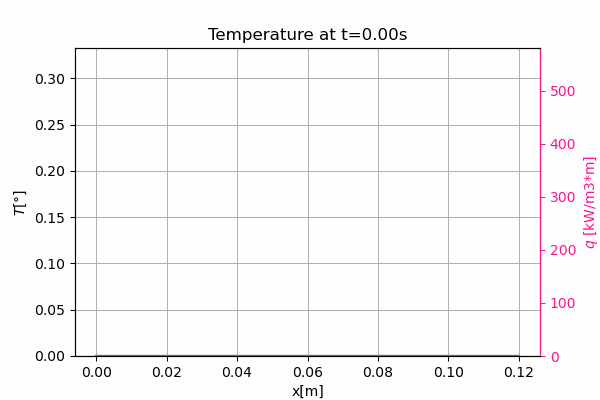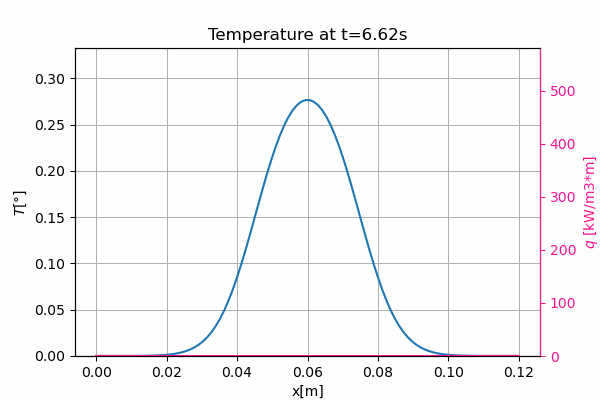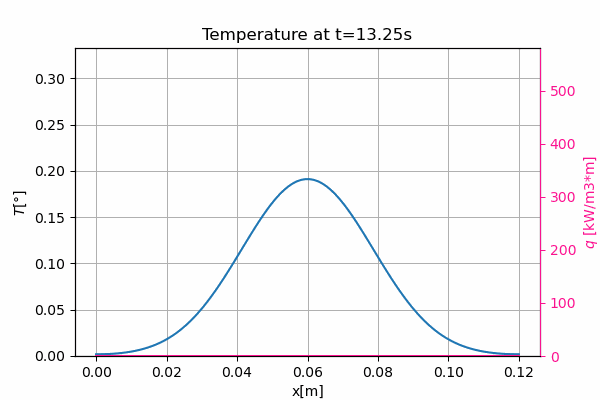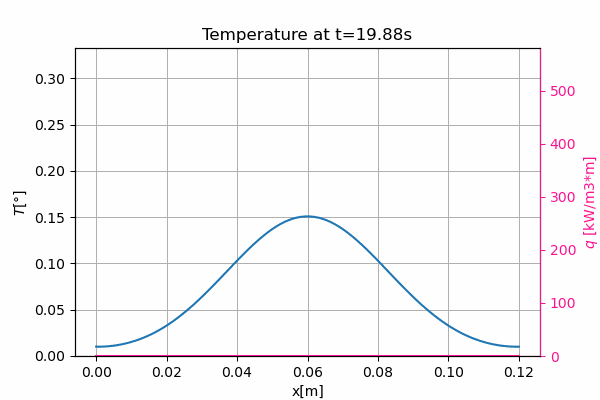
This is an example 1D conduction problem with temporary heating source and heat loss by convection all along the sample. No flux boundary conditions are considered at extremities.
Theoretical background¶
For this example let’s consider the 1D heat equation in its non-steady form:
$$ \rho c_p \frac{\partial T}{\partial t} = k \frac{\partial^2 T}{\partial x^2} + s(x,t) - h_b T $$
Where $\rho$ is the density, $c_p$ is the specific heat, $k$ is the thermal conductivity, $s(x,t)$ is the source term, and $h_b$ is a coefficient that allows to take into account the heat transfer coefficient by convection along the x-axis (it models the heat loss along by the side all along the sample).
Zero flux boundary conditions are considered at extremities ($x=0$ and $x=x_{max}$): $$ \left(\frac{\partial T}{\partial x}\right)_{x=0} = 0 $$ $$ \left(\frac{\partial T}{\partial x}\right)_{x=x_{max}} = 0 $$
Numerical resolution of the heat equation¶
To solve numerically this kind of PDE, an explicit integration scheme is often used (Euler, RK4, ...). But this may lead to numerical instabilities (the solution may diverge) if the time step is not small enough. The stability condition is given by the following equation: $$ \Delta t < \frac{\Delta x^2}{2 \alpha} $$ Where $\Delta t$ is the time step, $\Delta x$ is the spatial discretization step, and $\alpha$ is the thermal diffusivity ($\alpha = \frac{k}{\rho c_p}$).
One of the solutions to overcome this stability issues is to use an implicit integration scheme. To do so, in this example we used the EDO solver from scipy as time integration scheme. The python library scipy.integrate provides a large choice of integration scheme (explicite and implicite), here we use the BDF (Backward Differentiation Formula) scheme.
Formulation of the heat equation as an EDO system¶
The heat equation is formulated as a system of first order differential equations:
$$ \frac{\partial T}{\partial t} = \frac{k}{\rho c_p} \frac{\partial^2 T}{\partial x^2} + \frac{s(x,t)}{\rho c_p} - \frac{h_b}{\rho c_p} T $$
The system of equations can be solved using the EDO solver from scipy, we need to compute the Laplacian of the temperature field $\frac{\partial^2 T}{\partial x^2}$:
$$ \frac{\partial^2 T}{\partial x^2} = \frac{T_{i+1} - 2 T_i + T_{i-1}}{\Delta x^2} $$
Where $\Delta x$ is the spatial discretization step.
Implementation¶
Laplacian estimation function¶
for this function we used the @njit decorator from numba to speed up the computation.
import numpy as np
from numba import njit
@njit
def lap_loop(T):
NX = len(T)
Tp = np.zeros((NX))
for i in range(1, NX-1):
Tp[i]=((T[i-1] - 2. * T[i] + T[i+1]))
return Tp
Source function¶
The source function apply a volumes heat source in the middle of the sample ($45 mm<x<75 mm$) during 3s ($2s<t<5s$). The magnitude of the source is denoted by the $q$ parameter ($(W/m^3)*m$).
@njit
def source(x,t,q):
"""
source terms of the heat equation
"""
s = np.where((x>45e-3) & (x<75e-3) & (t>2.) & (t<5.), q, 0.)
return s
ODE diff function¶
The ODE diff function is the function that will be passed to the EDO solver, it takes as input the current temperature field, the current time and extra parameters. It returns derivative of $T$ respect to time $\frac{\partial T}{\partial t}$.
The zero flux boundary conditions are implemented into this function.
def Tp_1D(t, T, NX, x, dx, rhoCp, k, q, hb):
"""
compute DT/dt for the 1D heat eq
"""
Tp = np.zeros((NX))
# Laplacian estimation using finite difference method
coef = k / (dx**2)
Tp = coef * lap_loop(T)
# Heat loss by convective changes by the side of the sample hb = 2*hl / e
Tp -= hb * T # heat loss by convection on the side of the sample
# source term
Tp += source(x, t,q)
# BC
# zero flux at the extremities
Tp[0] = Tp[1]
Tp[NX-1] = Tp[NX-2]
# divide by rho*Cp
Tp /= rhoCp
return Tp
Physical parameters and simulation setup¶
Here we model the conduction in a sample made of steel. The dimensions of the sample are given in the data dictionary. In this dictionary we also define the physical parameters of the material and the simulation setup.
Some extra computations are made before solving the ODE system:
- the spatial discretization step $\Delta x$ is computed from the number of points in the spatial domain and the length of the sample
- the initial temperature field is set to zero
- the time vector is computed from the simulation time and the time step
Finally, the ODE system is solved using the scipy EDO solver.
import time
from scipy.integrate import solve_ivp
# data of the problem
data ={
"k": 50., # thermal conductivity [W/m/K]
"rho": 7850., # density [kg/m3]
"Cp": 465., # specific heat [J/kg/K]
"e": 1.55e-3, # thickness of the sample [m]
"l": 15e-3, # width of the sample [m]
"hl": 10., # heat transfer coefficient by convection [W/m2/K]
"t_max": 20., # duration of the simulation [s]
"x_max": 120e-3, # length of the sample [m]
"nt": 161, # number of time steps
"nx": 100,# number of space steps
"q" : 18/30e-3/1.55e-3, # source term [W/m3*m] (18 W applied on 30 mm length)
}
# exenage by convection on the side of the sample : hb = hl*P/A
P = 2*(data["e"]+data["l"])
A = data["e"]*data["l"]
hb = (data["hl"] * P/A)
# space and time discretization
x = np.linspace(0., data["x_max"], data["nx"])
dx= x[1]-x[0]
t_eval = np.linspace(0., data["t_max"], data["nt"])
# args to pass to the solver
rhoCp= data["rho"] * data["Cp"]
args = (data["nx"], x, dx, rhoCp, data["k"], data["q"], hb)
The boundary conditions are implemented into the ODE diff function. The initial temperature field is set to zero. $$ T(x,t=0) = 0 $$
It will be passed at the ODE solver as the initial condition.
T0 = np.zeros_like(x)
We have defined :
- the ODE function (with boundary conditions and source term)
- the initial condition
- the time and space discretization
- the physical parameters of the simulation
We can now solve the ODE system using the scipy EDO solver scipy.integrate.solve_ivp.
# time integration
print("Solve 1D heat equation")
t0 = time.time()
Duration = data["t_max"]
sol = solve_ivp(Tp_1D, [0, Duration],
T0,
t_eval=t_eval,
method='BDF',
vectorized=False,
args=args)
print("Done in {:.2f} s".format(time.time()-t0))
Solve 1D heat equation Done in 1.74 s
Plotting the results¶
The first plot shows the temperature field respect to time and space. The second plot the source term respect.
import matplotlib.pyplot as plt
%matplotlib ipympl
# create a figure with two subplots
cmap = "RdBu_r"
fig = plt.figure(figsize=(6, 12))
ax1 = fig.add_subplot(211, projection='3d')
ax2 = fig.add_subplot(212, projection='3d')
# create meshgrid for x and t
xg, tg = np.meshgrid(x, t_eval)
# plot the temperature on the first subplot
ax1.plot_surface(xg, tg, sol.y.T, cmap=cmap, edgecolor='none')
ax1.set_xlabel("x[m]")
ax1.set_zlabel(r"$\theta$ [°]")
ax1.set_ylabel("t[s]")
ax1.set_title("Temperature")
# plot the source on the second subplot
ax2.plot_surface(xg, tg, source(xg, tg, data["q"])/1000, cmap=cmap, edgecolor='none')
ax2.set_xlabel("x[m]")
ax2.set_zlabel(r"$q$ [kW/m3*m]")
ax2.set_ylabel("t[s]")
ax2.set_title("Source")
# adjust the spacing between subplots
plt.subplots_adjust(wspace=0.3)
# display the figure
plt.show()
The heat spot can be seen in the middle of the sample. It results in a temperature increase of about $0.3°$, followed by a decrease due to the heat loss by convection.
We can also animate the temperature field evolution over time using the animate :
import matplotlib.animation as animation
from IPython.display import HTML, display
s = source(xg, tg, data["q"])/1000
T = sol.y.T
fig = plt.figure(figsize=(6, 4))
ax1 = fig.add_subplot(111)
ax1.set_ylim(T.min(), 1.1*T.max())
ax1.set_xlabel("x[m]")
ax1.set_ylabel(r"$T [°]$")
ax1.set_title("Temperature")
p1, = ax1.plot(x, T[0,:])
ax2 = ax1.twinx()
ax2.set_ylabel(r"$q$ [kW/m3*m]")
ax2.set_ylim(s.min(), 1.5*s.max())
ax2.spines['right'].set_color('deeppink')
ax2.tick_params(axis='y', colors='deeppink')
ax2.yaxis.label.set_color('deeppink')
p2, = ax2.plot(x, s[0,:], color='deeppink')
ax1.grid()
def update_plot(frame_number):
p1.set_ydata(T[frame_number,:])
p2.set_ydata(s[frame_number,:])
ax1.set_title("Temperature at t={:.2f}s".format(t_eval[frame_number]))
return p1, p2
anim = animation.FuncAnimation(fig, update_plot, frames = len(t_eval)-1, interval=100, blit=False)
plt.close(anim._fig)
display(HTML(anim.to_jshtml()))
And save it for later use:
# To save the animation using Pillow as a gif
writer = animation.PillowWriter(fps=15,
metadata=dict(artist='ERoux'),
bitrate=1800)
anim.save('HeatODE.gif', writer=writer)
Conclusion¶
This example shows how to solve the heat equation using the EDO solver from scipy. Some numerical difficulties are managed by the ODE solver which makes the implementation easier.
This example deals with 1D heat conduction, but the same approach can be used for 2D and 3D heat conduction.